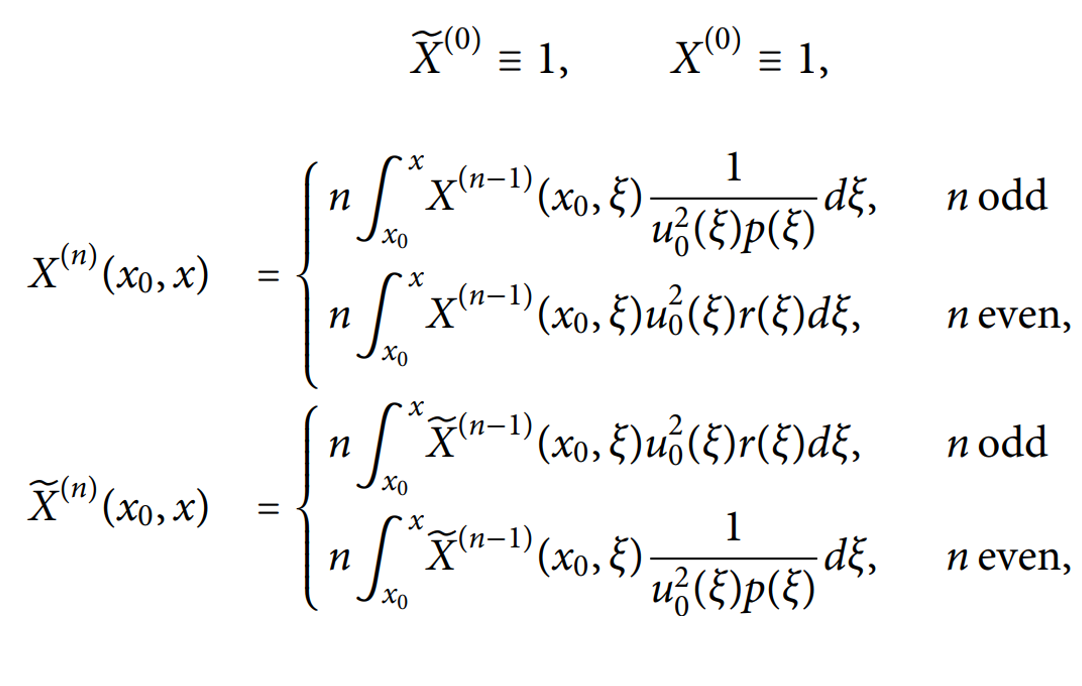
Supersymmetric generalized power functions.
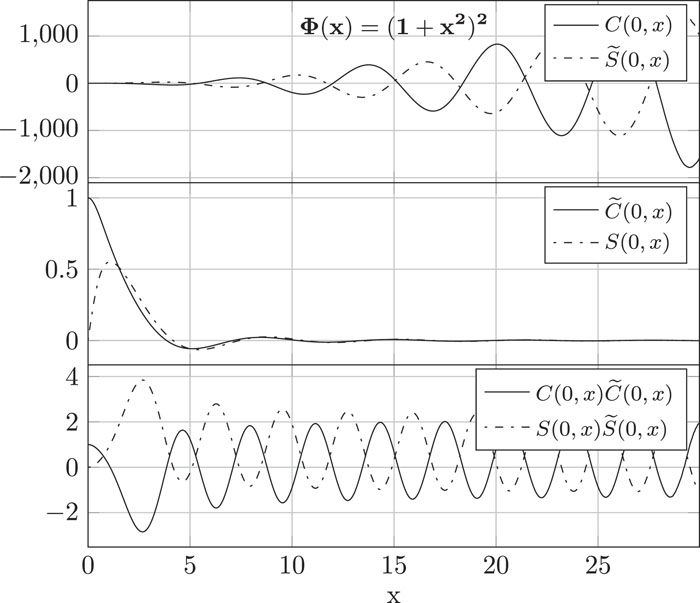
Generalized Φ-trigonometric functions.
Supersymmetric quantum mechanics (SUSYQM) explores the intriguing interplay between quantum mechanics and symmetry principles. This field extends traditional quantum mechanics by introducing supersymmetry, a framework where bosons and fermions—two fundamental particle types—are treated symmetrically. In SUSYQM, the mathematical structures and tools often reveal deeper physical insights, bridging gaps between mathematical abstraction and physical phenomena.
This work delves into the mathematical foundations of supersymmetric quantum mechanics (SUSYQM), focusing on the development and analysis of Φ-generalized power functions. These functions, constructed as natural solutions for SUSYQM systems, generalize traditional power functions to incorporate the unique symmetry properties of supersymmetric Hamiltonians. By leveraging the ground-state wave function, these generalized functions serve as the backbone for constructing solutions to one-dimensional quantum systems.
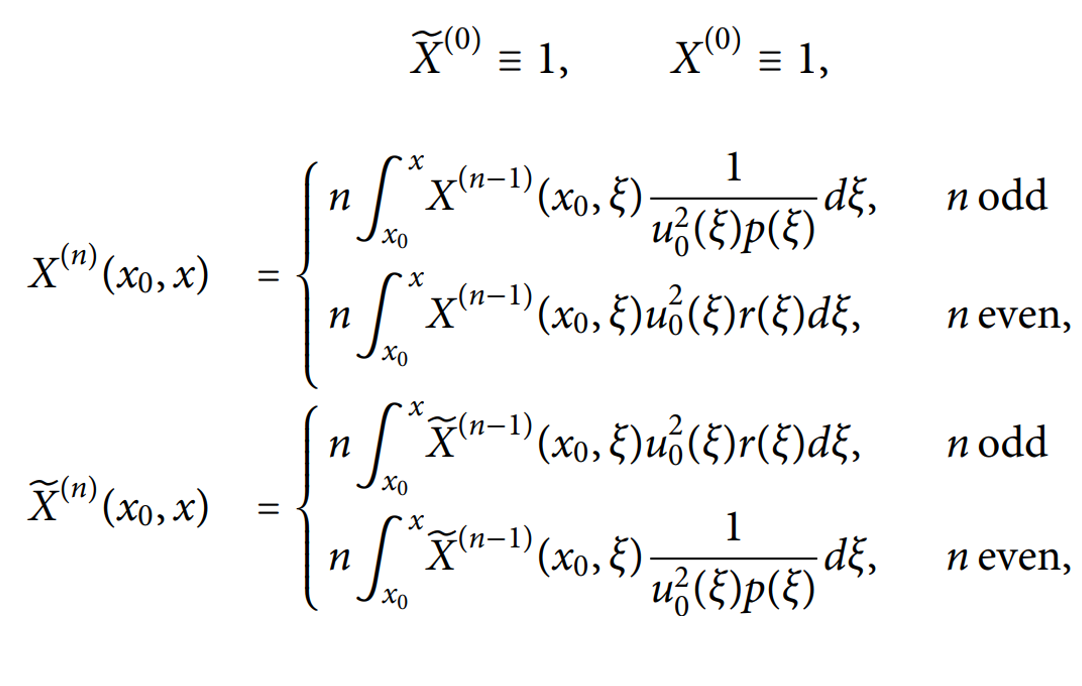
Supersymmetric generalized power functions.

Generalized Φ-trigonometric functions.
[1] Ouellet, M., & Tremblay, S. (2020). Supersymmetric generalized power functions. Journal of Mathematical Physics, 61(7).
[2] Ouellet, M., & Tremblay, S. (2019). Generalized power functions for one-dimensional supersymmetric quantum mechanics. ArXiv Preprint ArXiv:1905.07509.
[3] Ouellet, M. (2019). Les fonctions de puissances Φ-généralisées et leurs applications. (Thesis)